La foret puit de carbonne ? Une étude récente tend à montrer le contraire

Traduction automatique

Résumé

La végétation terrestre absorbe actuellement de grandes quantités de CO ₂ atmosphérique, probablement en raison de la stimulation de la croissance des arbres. Les modèles existants prédisent que cette stimulation de la croissance continuera de provoquer une absorption nette de carbone ce siècle. Cependant, il y a des indications que des taux de croissance accrus peuvent raccourcir la durée de vie des arbres et, par conséquent, les augmentations récentes des stocks de carbone forestier peuvent être transitoires en raison des augmentations retardées de la mortalité. Nous montrons ici que les compromis entre la croissance et la durée de vie sont en effet presque universels, se produisant dans presque toutes les espèces et tous les climats. Ce compromis est directement lié à une croissance plus rapide réduisant la durée de vie des arbres, et non à une covariance avec le climat ou l'environnement. Ainsi, la stimulation actuelle de la croissance des arbres entraînera inévitablement une augmentation retardée de la mortalité des arbres de la canopée, comme cela est effectivement largement observé, et finira par neutraliser les gains de carbone dus à la stimulation de la croissance.Les résultats d'un simulateur forestier fortement basé sur les données confirment ces attentes. Les projections du modèle existant du système terrestre de la persistance des puits de carbone forestiers mondiaux sont probablement trop optimistes, ce qui augmente la nécessité de réduire les émissions de gaz à effet de serre.

introduction

Au cours des 50 dernières années, les écosystèmes terrestres ont été responsables de l'élimination d'environ un tiers des émissions anthropiques de carbone ^{1 , 2} . Cette absorption nette de carbone a été attribuée à une combinaison de boisement et d'expansion des forêts secondaires ³ , ainsi qu'à d'éventuels changements dans la dynamique des forêts dus au dépôt d'azote et à l'augmentation du CO ₂ atmosphérique et de la température. En particulier, l'augmentation du CO ₂ et de la température, dans les régions froides, a été suggérée comme la cause de la croissance des arbres stimulée, entraînant un déséquilibre entre les taux de croissance et de mortalité et l'absorption nette de carbone même dans les forêts primaires ^{2 , 4}. Il est donc probable que les forêts aient contribué à ralentir les taux de croissance du CO ₂ atmosphérique causés par la combustion de combustibles fossiles et la fabrication de ciment, et sur la base des prévisions des modèles du système terrestre ^{5 , 6} devraient largement continuer à jouer ce rôle dans le futur. Cependant, la mesure dans laquelle les forêts continueront d'absorber l'excès de CO ₂ atmosphérique dépend non seulement de la réponse de croissance des arbres à un climat changeant et de la composition atmosphérique, mais aussi des changements dans les taux de mortalité qui rejettent finalement du carbone dans l'atmosphère ^{7 , 8 , 9} . Augmentation de la croissance des arbres due par exemple au CO ₂, l'augmentation de la température, des dépôts d'azote ou de la durée de la saison de croissance doit éventuellement entraîner une augmentation de la mortalité des arbres ¹⁰ . Cette rétroaction négative sur le stockage du carbone via une mortalité accrue compensera - au moins dans une certaine mesure - les effets bénéfiques d'une croissance accrue sur le stockage total du carbone des forêts ^{9 , 10} . Notre connaissance actuelle et incomplète de l'universalité et des causes de la rétroaction entrave sa représentation dans les modèles du système terrestre et constitue donc une incertitude importante dans les prévisions de l'absorption future de carbone des forêts en réponse au changement global ^{7 , 8 , 9 , 11} .

Les données de surveillance permanente des parcelles forestières montrent des augmentations généralisées de la mortalité, qui ont été proposées comme étant liées aux augmentations de croissance ^{4 , 12} . Cependant, un lien direct entre les tendances de croissance et de mortalité ne peut généralement pas être établi en utilisant uniquement les données de surveillance, car la détection de cette rétroaction démographique dans les arbres à longue durée de vie dépasse souvent la durée pendant laquelle les données d'inventaire ont été recueillies. À l'heure actuelle, la seule méthode pratique pour évaluer la réponse de la durée de vie à la croissance d'organismes à longue durée de vie comme les arbres consiste à utiliser des cernes annuels. Pour toutes les espèces, des études sur les cernes ont montré il y a longtemps qu'il y a un compromis entre la croissance et la durée de vie des arbres ^{13 , 14}. Ce compromis a été attribué à une partition de l'allocation des ressources à la croissance par rapport à la survie et est un axe bien connu de stratégies végétales allant des espèces pionnières à croissance rapide à une extrémité, et à croissance lente à plus longue durée de vie, à l'ombre ou espèces tolérantes à la sécheresse à l'autre extrémité ^{15 , 16} . Un nombre croissant d'études ont démontré que des compromis similaires se produisent également au sein des espèces, les individus à croissance plus rapide ayant une durée de vie plus courte ^{17 , 18 , 19 , 20 , 21} . Cependant, ces études se sont principalement concentrées sur les conifères à haute altitude ^{19 , 21} , ou n'incluent qu'un nombre limité d'espèces boréales et tempérées^{17 , 18 , 20} . Certains rapports suggèrent même un manque de tels compromis^{22 , 23} . Ainsi, les preuves du phénomène de compromis entre la croissance et la durée de vie et l'étendue de son apparition dans les biomes et les taxons d'arbres sont encore incomplètes. En outre, les connaissances sur les mécanismes par lesquels les arbres à croissance rapide tendent à mourir plus tôt et l'ampleur de son effet sur la mortalité des forêts et le puits de carbone terrestre restent incertaines.

Ici, nous utilisons les données des anneaux d'arbres pour montrer que des compromis entre la croissance précoce et la durée de vie se produisent pour une large gamme d'espèces et d'environnements. Une croissance plus rapide réduit directement la durée de vie d'un arbre et peut expliquer les augmentations observées de la mortalité des arbres. En utilisant des simulations de modèles, nous constatons que ce compromis a des répercussions potentiellement importantes sur le futur puits de carbone.

résultats et discussion

Observations des compromis croissance-durée de vie à l'échelle mondiale

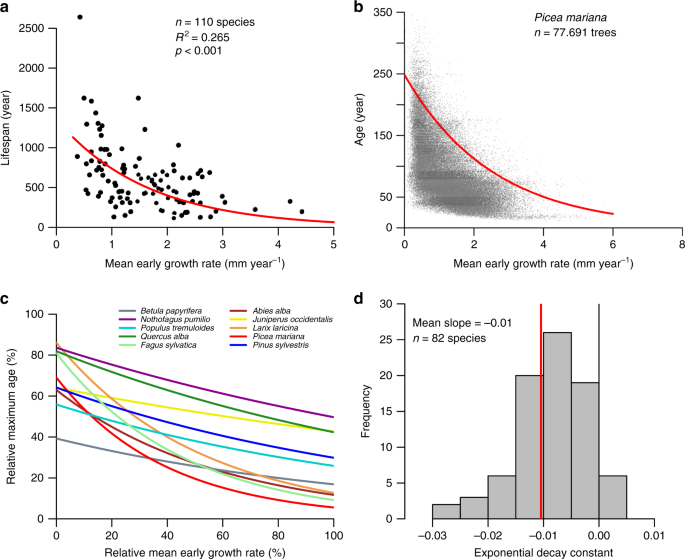
Nous compilons et analysons ici des ensembles de données sur les cernes comprenant 110 espèces différentes des tropiques aux hautes latitudes pour évaluer l'existence de compromis croissance-durée de vie (voir «Méthodes»). Nous constatons que les taxons avec des taux de croissance rapide et précoce ont une durée de vie maximale courte et vice versa ( Fig.1a ), confirmant un compromis largement connu entre ces caractères à travers les espèces ^{13 , 15} . Les relations au niveau de l'arbre, au sein des espèces, montrent des relations remarquablement similaires entre la croissance précoce et la durée de vie (Fig. 1b – d ). Par exemple, dans Picea mariana du Québec ( Fig.1b), une croissance rapide et précoce sélectionne fortement les arbres qui atteignent la vieillesse, tandis que les âges les plus anciens de cet ensemble de données proviennent majoritairement d'arbres qui poussaient lentement lorsqu'ils étaient jeunes (figure supplémentaire 3 ). Pour presque toutes les espèces examinées (74 sur 82), la croissance précoce et la durée de vie étaient anticorrélées (Fig. 1c, d et Fig. 4 supplémentaire ). En moyenne, la durée de vie des arbres a diminué de façon exponentielle avec une réduction de 23% de la durée de vie pour une augmentation de la croissance précoce de 50%. La force moyenne de la constante de désintégration du compromis était similaire entre différents taxons (gymnospermes vs angiospermes) et entre les zones climatiques (boréale, tempérée et tropicale) (Fig. 5a-e supplémentaire) ). Étant donné que notre échantillon comprend des espèces d'habitats allant des forêts tropicales humides à canopée fermée aux forêts arctiques ouvertes, ces résultats remarquables suggèrent que les compromis ne se limitent pas à quelques espèces spécifiques ou à des habitats particuliers. Nos analyses confirment également que les compromis observés ne sont pas le résultat de biais dus à une concentration sur les échantillons d'arbres vivants (Fig. 5f, g supplémentaire ) ou à la sélection de grands arbres (Fig. 6 supplémentaire ). La découverte d'une durée de vie toujours plus longue pour les arbres à croissance lente peut sembler en contradiction directe avec les observations répétées d'un risque de mortalité plus élevé pour les arbres à croissance lente qui sont supprimés ou qui ont subi une autre forme de dommage qui n'a pas tué initialement les arbres ^{22 , 23 ,24 , 25} . Ces résultats apparemment contradictoires peuvent cependant être conciliés par des différences dans les analyses effectuées et les ensembles de données utilisés. Nous n'avons utilisé que des essences rigoureusement sélectionnées pour lesquelles nous avions un très grand nombre de grands arbres. Ainsi, notre analyse inclura avec une forte probabilité les arbres les plus longs pour un large éventail de catégories de croissance précoce, et nous permettra d'effectuer desrégressions quantiles du95^e pour estimer la durée de vie des arbres. Contrairement aux études précédentes^{22 , 23 , 24 , 25}, notre approche est relativement insensible aux processus de mortalité aux stades précoces et intermédiaires, qui sont régis par des baisses de croissance avant la mort. Nous concluons ainsi que les compromis entre la croissance et la durée de vie au sein des espèces ne sont probablement pas détectables à l'aide de la plupart des données d'inventaire forestier ou de la télédétection, et pourtant sont un phénomène universel et important qui influence le fonctionnement des forêts à l'échelle mondiale.

**Fig. 1: Relation entre le taux de croissance et la durée de vie maximale dérivée des anneaux des arbres.**

Contrôles environnementaux du compromis

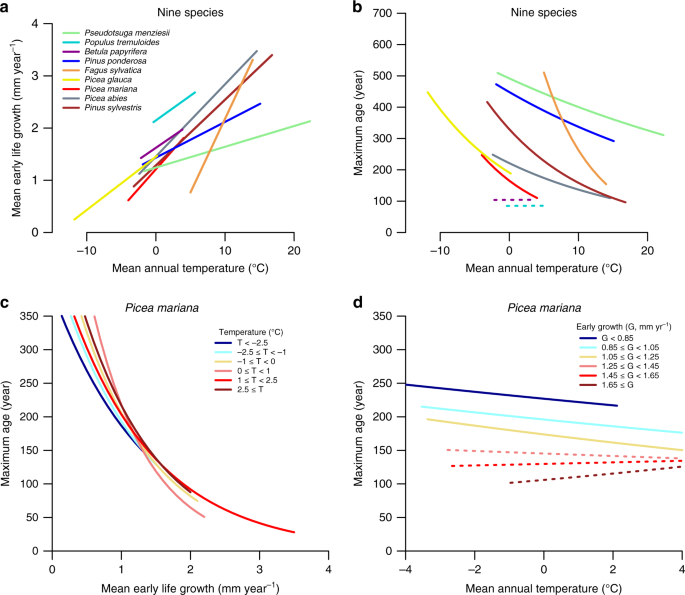
Plusieurs études ont rapporté que la durée de vie est fortement corrélée avec des variables environnementales comme la durée de la saison de croissance et la température de l'air ²⁰ . Dans cette optique, nous trouvons des corrélations négatives entre la durée de vie et la température annuelle moyenne pour un certain nombre d'espèces (Fig. 2a, b et Fig. 7 supplémentaire ). Cela soulève la possibilité que les compromis entre la croissance et la durée de vie soient contrôlés par des variables environnementales externes, comme la température, et ne soient pas dus à une croissance plus rapide influençant directement la probabilité de mortalité. Nous soutenons, cependant, que ce n'est pas le cas avec deux éléments de preuve. Premièrement, nos analyses approfondies de l'ensemble de données pour Picea marianadu Québec montre que, tandis que la durée de vie et la croissance covarient avec diverses variables environnementales, y compris la température (Fig. 2c, d ), le type de sol, et la couverture de couronne (Fig supplémentaire. 8 ), et non pas un seul facteur explique entièrement la variation du taux de croissance et durée de vie. De même, nous avons observé des compromis comparables dans les espèces qui poussent dans des écosystèmes avec des limitations de croissance intrinsèquement différentes, y compris les forêts boréales qui sont principalement contrôlées par la température ( Fig.2a ), les plaines inondables tropicales avec de forts contrôles édaphiques ²⁶ et les forêts à couvert fermé avec des niveaux élevés. de compétition pour la lumière ^{20 , 27}. Deuxièmement, les compromis entre la croissance et la durée de vie sont restés solides même après avoir pris en compte les facteurs environnementaux possibles. Par exemple, pour Picea mariana du Québec, il n'y a pas eu de changement substantiel dans les compromis entre la croissance et la durée de vie lorsque nous avons regroupé les données par température, alors que les relations entre la durée de vie et la température se décomposent en grande partie lorsque les données ont été regroupées par taux de croissance (figures 2c, d ). Des résultats similaires sont obtenus pour cette espèce pour les autres variables de l' environnement de contrôle comme la couverture de la couronne et le type de sol (Fig supplémentaire. 8). Pour la plupart des espèces, nous trouvons des modèles très similaires avec des effets robustes de la croissance au début de la vie sur la durée de vie, même en contrôlant la température (mais pas l'inverse, voir les méthodes). Au total, ces analyses prouvent que le taux de croissance est intrinsèquement lié à la durée de vie des arbres, ce qui explique pourquoi des compromis sont en fait trouvés entre des espèces de taxons phylogénétiquement éloignés et poussant dans des environnements très différents.

**Fig. 2: Effet de la température sur la croissance précoce et la durée de vie des arbres.**

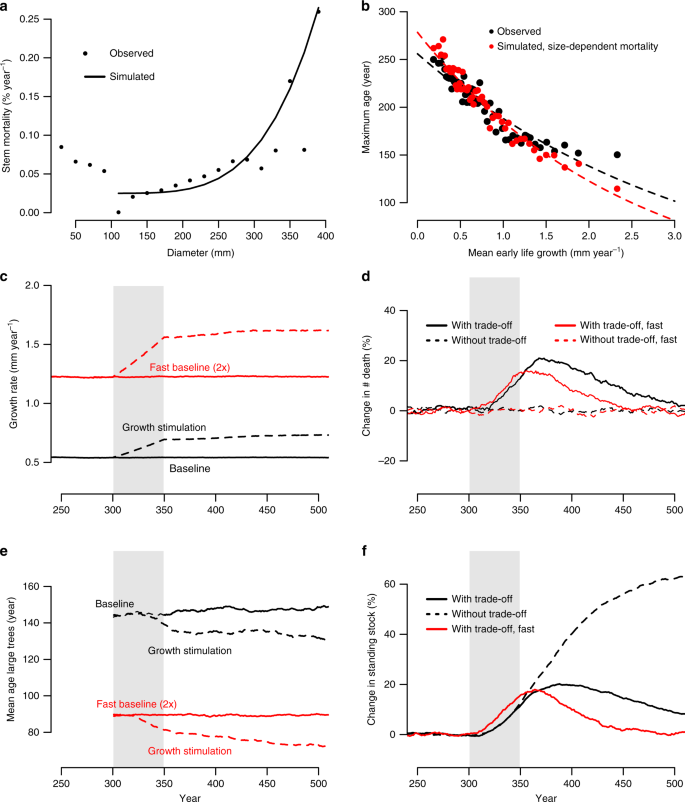
Diverses théories ont été proposées pour expliquer les compromis croissance-durée de vie au sein d'une espèce. La première théorie est qu'une croissance plus rapide nécessite des taux de métabolisme cellulaire plus élevés qui peuvent avoir des effets directement négatifs sur la durée de vie des arbres. Cette théorie a également été appelée «théorie du taux de vie» et est connue pour expliquer la variation de la durée de vie au sein des clades d'animaux ²⁸ . Elle s'applique également aux plantes ligneuses au niveau de l'organe ²⁹ . Cependant, il a été observé que les cellules végétales ne font pas de sénescence au sens strict comme le font les cellules animales ³⁰ . Les cellules du méristème des plantes se divisent continuellement à des taux relativement faibles et ne montrent aucune détérioration réelle de leur fonction, même dans les très vieux arbres tels que les pins bristlecone (~ 4800 ans) ³¹. Deuxièmement, les arbres peuvent être confrontés à un compromis direct entre l'allocation à la croissance par rapport à l'investissement dans une architecture mécanique et hydraulique plus sûre et un investissement plus important dans les défenses. Ainsi, le développement de caractères qui augmentent la survie des espèces peut entraîner des taux de croissance plus faibles ^{13 , 15 , 16} . Bien que cela ait été observé à travers les espèces, on ne sait pas dans quelle mesure cela pourrait expliquer la variation intra-espèce de la croissance et de la durée de vie. La variation des traits essentiels à la survie des plantes tels que la densité du bois, l'architecture hydraulique et la résistance aux ravageurs et aux agents pathogènes peut être importante, même au sein des espèces ³², mais il reste encore à explorer en détail comment ces traits coïncident avec la croissance et la longévité des arbres. En effet, les preuves provenant d'une espèce de conifères indiquent que la survie lors d'une épidémie de scolytes ou d'une sécheresse était associée à de faibles taux de croissance et à des caractères conférant une plus grande résistance au scolyte ou une plus grande sécurité hydraulique, respectivement ^{33 , 34} . Une troisième théorie est que les compromis entre la croissance précoce et la durée de vie surviennent simplement parce que les arbres à croissance rapide atteignent leur taille maximale potentielle plus tôt. Les observations montrent que la mortalité des arbres augmente en effet à mesure que les arbres grandissent ^{35 , 36} , alors qu'il a été démontré que l'âge des arbres est un mauvais indicateur de la performance physiologique des arbres, par rapport à la taille des arbres ³⁰. Si cela est vrai, nous nous attendons à ce que la taille maximale des arbres pour des conditions climatiques et édaphiques données soit largement indépendante des taux de croissance. C'est en effet ce que nous trouvons pour Picea mariana , car les arbres à croissance rapide et lente de cette espèce atteignent approximativement la même taille maximale (~ 300 mm), mais le font à des âges sensiblement différents (Fig. 3 supplémentaire ). Comme nous le montrons dans la section suivante, en effet, des simulations simples avec des données observées sur les cernes et des taux de mortalité augmentant avec la taille, s'approchant d'un maximum absolu potentiel, aboutissent à une relation croissance-durée de vie très similaire à celle observée (Fig. 3b ). En revanche, les fonctions de mortalité dépendant de l'âge ne reproduisent pas le compromis croissance-durée de vie ( Fig.9a, b). Ainsi, l'existence d'une taille d'arbre potentielle maximale fournit une explication plausible pour au moins une partie du compromis observé. La taille maximale de l'arbre est un caractère spécifique à l'espèce, et peut-être au site ³⁷ , mais ce qui tue finalement un arbre une fois qu'il dépasse sa taille potentielle maximale peut impliquer une limitation hydraulique ^{38 , 39 , 40} , une stabilité mécanique, un déséquilibre entre la photosynthèse et la respiration d'entretien, et vulnérabilité croissante aux agents pathogènes et aux épidémies d'insectes ⁴¹ . Alors que les observations empiriques des courbes de taille de mortalité en U ^{35 , 36} soutenir ce mécanisme, nous devons établir les détails de chaque mécanisme potentiel à travers diverses espèces pour comprendre le potentiel émergent de ces compromis pour affecter considérablement le potentiel de stockage futur du carbone dans les forêts.

**Fig. 3: Relations entre diamètre-mortalité et taux de croissance-durée de vie pour *Picea mariana* , et résultats de simulation.**

Implications pour la démographie forestière et le puits de carbone

Nous avons évalué l'effet des compromis observés entre la croissance et la durée de vie sur la dynamique des forêts à l'aide d'un simulateur de forêt stochastique simple basé sur des données pour Picea mariana . Notre approche a consisté à créer une population artificielle en sélectionnant au hasard des trajectoires de cernes, en appliquant une mortalité liée à la taille et une stimulation de croissance réaliste (Fig. 3c ). La courbe de mortalité liée à la taille appliquée correspond étroitement aux taux de mortalité estimés liés à la taille pour Picea mariana ( Fig.3a ), et aboutit à des compromis croissance-durée de vie similaires à ceux observés ( Fig.3b). Nous avons ensuite comparé la variation de la biomasse et de la mortalité au fil du temps pour des simulations qui incluent un compromis (causé par la mortalité dépendante du diamètre), avec des simulations qui ne donnent pas lieu à un compromis croissance-durée de vie (en utilisant les taux de mortalité liés à l'âge, Supplémentaire Fig. 9 ), et qui ressemblent aux approches couramment utilisées par les modèles de végétation à grande échelle qui prédisent de grandes augmentations de la biomasse ⁵ . Notre croissance augmentation simulée estimée moyenne (diamètre) de plus de 50 ans en raison du réchauffement de latitude nord est de 29%, à peu près conforme à température observée augmente de croissance conduit de 25% au cours des 50 dernières années dans les forêts de l' Ouest canadien boréales ⁴² et les changements de croissance prévus au Nord latitudes ⁴³ .

Nos simulations montrent une augmentation initiale d'environ 20% des stocks de biomasse sur pied et des augmentations des taux de mortalité d'une ampleur similaire. Bien que sondes de stimulation de la croissance à une augmentation immédiate des stocks de biomasse, la mortalité commence à augmenter un ou deux ans après la stimulation de la croissance initiale (Fig. 3). La conclusion la plus importante de notre simulation, cependant, est que l'augmentation initiale des stocks de biomasse, le puits de carbone potentiel net, n'est que transitoire et se transforme en pertes nettes de biomasse après la fin de la stimulation de la croissance. Au fil du temps, les stocks de biomasse forestière reviennent aux mêmes niveaux que ceux observés au début de la simulation. Cette progression vers les valeurs initiales est entièrement due à une croissance plus rapide des arbres conduisant à une réduction de la durée de vie des arbres jusqu'à 23 ans après l'arrêt de la stimulation de la croissance (Fig. 3e ). En revanche, nous ne trouvons aucune augmentation de la mortalité pour les simulations sans compromis réaliste entre la croissance et la durée de vie (c.-à-d. Mortalité dépendante de l'âge, cf. Fig. 3d), et trouvent des augmentations de stock de biomasse beaucoup plus élevées qui se maintiennent dans le temps, même après l'arrêt de la stimulation de la croissance (Fig. 3f ).

Ces simulations basées sur les données suggèrent qu'une croissance plus rapide entraînera une augmentation de la mortalité des tiges, un cycle plus rapide de la biomasse vivante et aucune augmentation réelle à long terme des stocks de biomasse. Les simulations reposent sur plusieurs hypothèses simplifiées. Premièrement, nous n'avons simulé aucun effet de compétition, ni changement dans le recrutement des arbres. On pourrait soutenir que les changements climatiques ou l' augmentation du CO ₂ auront une incidence sur le recrutement et que l'augmentation des stocks de biomasse sur pied augmentera les effets de la concurrence, menant à une auto-éclaircie accrue et à des augmentations encore plus fortes des taux de mortalité. Deuxièmement, nous supposons que la courbe de mortalité liée à la taille est indépendante des changements de température ou de CO ₂ , ce qui peut ne pas être vrai. À notre connaissance, il n'y a aucune preuve que la taille maximale potentielle des arbres peut augmenter sous un CO₂ , alors que l'augmentation des déficits de pression de vapeur feuille-air sous l'effet du réchauffement climatique a été supposée entraîner une réduction de la hauteur maximale des arbres ⁴⁴ . Il n'est donc pas clair comment les effets interactifs du CO ₂ et de la température affecteront la stature potentielle maximale des arbres, mais il est moins probable que la taille maximale des arbres augmente. Un scénario plus probable qui pourrait potentiellement expliquer un plus grand stockage futur du carbone forestier sous l'augmentation du CO ₂ est que les relations taille-densité des arbres pourraient être modifiées ⁴⁵ , bien que les données empiriques à long terme montrent que la règle d'auto-éclaircie n'a pas changé malgré de fortes augmentations de croissance au fil du temps ⁴⁶. Enfin, la distribution des espèces est susceptible de changer en réponse au changement climatique, en particulier dans les latitudes moyennes à élevées, et affectera la quantité totale de biomasse qu'un système peut contenir ⁴⁷ . Malgré ces simplifications, les résultats de nos simulations sont cohérents avec les prévisions basées sur des modèles forestiers démographiques plus complexes qui ne prédisent aucune augmentation nette de la biomasse ⁹ ou des augmentations fortement réduites en incluant une rétroaction négative sur la stimulation de la croissance ^{7 , 48} . Nos résultats présentent également une forte similitude avec certaines observations de l'évolution de la dynamique des forêts dans le monde. Premièrement, des études de suivi sur le terrain ont montré des tendances positives simultanées des taux de croissance et de mortalité à travers le monde ^{49 , 50}. Les forêts boréales à température limitée ont connu des augmentations de croissance ⁴² et des augmentations de mortalité simultanées ^{12 , 51} , les forêts d'Europe centrale montrent des augmentations de croissance au cours des dernières décennies, ce qui a entraîné une dynamique forestière accélérée ⁴⁶ , et les forêts amazoniennes non perturbées ont connu des améliorations de productivité à long terme, suivies par d'autres la mortalité récente augmente avec un retard d'environ 20 ans ⁴ . Certaines de ces tendances de mortalité ont été attribuées à la variabilité du climat, en particulier à des changements dans la gravité et la fréquence des sécheresses ^{4 , 49 , 51}. Cependant, nous suggérons ici que l'augmentation de la mortalité n'est pas seulement une conséquence directe de l'augmentation de la variabilité climatique, mais qu'elle peut également découler en fin de compte des compromis omniprésents entre la croissance et la durée de vie qui ont accéléré le moment de la mort des grands arbres.

En résumé, nous fournissons ici des preuves solides de l'existence d'un compromis universel entre la croissance précoce et la durée de vie des arbres. Une croissance plus rapide a un effet direct et négatif sur la durée de vie des arbres, indépendamment des mécanismes environnementaux entraînant la variation du taux de croissance. Les augmentations de croissance, comme récemment documentées dans les forêts de haute latitude et tropicales, devraient donc réduire la durée de vie des arbres et pourraient expliquer les augmentations observées de la mortalité des arbres dans ces biomes. Les simulations basées sur les données montrent que les compromis ont le potentiel de réduire, voire d'inverser le puits de carbone mondial des forêts à l'avenir. Ce mécanisme est en contradiction avec la plupart des simulations existantes du modèle du système terrestre, qui prédisent la poursuite du puits de carbone dans les forêts matures ⁵Par conséquent, les efforts visant à intégrer les compromis taux de croissance-mortalité dans les simulations de processus de stockage du carbone forestier devraient recevoir une plus grande attention.

Méthodes

Données de l'anneau d'arbre

Nous avons utilisé des enregistrements cycliques d'arbre de plus de 210.000 arbres de 110 espèces, réparties globalement dans des habitats allant de la zone tropicale de l'Arctique sur plus de 70.000 sites (Fig supplémentaire. 1 , supplémentaires Tableau 1 ). La plus grande source de données accessible au public à partir de laquelle nous avons utilisé des données est la Banque internationale de données sur les cernes (ITRDB, https://www.ncdc.noaa.gov/data-access/paleoclimatology-data/datasets/tree-ring ). Celles-ci ont été complétées par d'autres ensembles de données pour maximiser le nombre d'enregistrements pour chaque espèce et pour combler les lacunes spatiales. Les données de l'Inventaire forestier national du ministère des Forêts de la Faune et des Parcs du Québec, Canada ⁵²^,^{53 constituent un} ensemble de données particulièrement volumineux sur les cernes utilisés dans nos analyses ^.(ci-après NFI-Québec). Ces données consistent en un ensemble complet de données sur la largeur des anneaux provenant de 156 711 arbres provenant de 79 381 sites à travers la province de Québec. Les données sur les cernes d'arbres de terrain ont été collectées selon des protocoles standards spécifiques ^{52 , 53} , qui consistaient à sélectionner jusqu'à neuf arbres dans chaque parcelle, avec 3 à 5 arbres (> 91 mm de diamètre à hauteur de poitrine, DBH) sélectionnés au hasard, 1– 2 choisis parmi les plus grands arbres et 1–2 parmi les arbres les plus proches du diamètre moyen des arbres de la parcelle ^{52 , 53} . Des arbres sélectionnés, un noyau par arbre a été collecté. Les données sur les cernes d'arbres tropicaux ont été compilées à partir de l'ITRDB et à partir de documents non publiés et publiés ^{26 , 27 , 54 , 55}. Pour les espèces avec des échantillons de plus grande taille, nous avons fait une distinction entre les données sur les cernes d'arbres morts naturellement avant le moment de l'échantillonnage et les arbres qui étaient vivants au moment de l'échantillonnage, ce qui nous permet de tester l'hypothèse selon laquelle l'âge des arbres vivants peut être utilisé pour estimer durée de vie naturelle des arbres (voir la section «Estimations des compromis et évaluation des artefacts possibles»). Une partie de ces données sur les arbres morts a été obtenue de l'ITRDB en sélectionnant des enregistrements de cernes dont la dernière largeur de cerne mesurée était datée d'avant l'an 1900. Nous avons supposé que la plupart de ces arbres devaient être morts au moment de l'échantillonnage, car aucun enregistrement n'avait été recueilli avant 1900. De plus, nous avons compilé les données publiées sur les arbres morts à partir des références. ^{21 , 56} , et utilisé les données de cernes d'arbres sous-fossiles des réf. ^{57 ,58} . Le tableau supplémentaire 1 donne un aperçu des ensembles de données, et les détails complets de chaque ensemble de données sont disponibles en ligne en tant qu'informations supplémentaires.

Divers contrôles de données et procédures de sélection ont été utilisés pour assurer une confiance élevée dans notre ensemble de données. Dans la mesure du possible, nous avons essayé d'identifier des enregistrements en double, c'est-à-dire des cœurs multiples prélevés sur le même arbre individuel. C'est un problème uniquement pour l'ITRDB, mais pas pour l'ensemble de données NFI-Québec où il n'existait qu'un seul noyau par arbre, ou pour les ensembles de données des co-auteurs. Nous avons ainsi fusionné les enregistrements ITRDB qui avaient des ID identiques à l'exception du dernier caractère de leur ID (par exemple 01a, 01b ou ID1-1, ID1-2, etc.). À partir de l'ITRDB, nous n'avons utilisé que des espèces pour lesquelles nous pouvions obtenir des données d'un minimum de 3 sites différents avec au moins 20 enregistrements chacun, et uniquement des espèces sélectionnées qui avaient un total minimum de 100 séries de largeurs d'anneaux distinctes. Nous avons exclu les sites de l'ITRDB qui présentaient des structures d'âge relativement égales,et sont donc peu susceptibles de représenter des populations anciennes qui fournissent des estimations fiables de la durée de vie maximale des arbres. Pour cela, nous avons calculé pour chaque site ITRDB le coefficient de variation des âges des arbres (CV_Age = StandDev _Age/ Mean _âge x 100) et les sites exclus avec un CV d' _âge inférieur à 10%. Un grand sous-ensemble de données ITRDB de 46 espèces a déjà été inspecté pour la qualité des données par le co-auteur S. Voelker ⁵⁹ . Dans ce sous-ensemble de données, chaque série de largeur d'anneau a été ré-alignée manuellement en fonction de l'âge cambial (c.-à-d. Le nombre d'anneaux à partir de la moelle), fournissant des estimations plus fiables de l'âge des arbres. Pour les ensembles de données qui n'ont pas été acquis auprès de l'ITRDB, nous avons utilisé des critères légèrement différents. De NFI-Québec, nous avons utilisé tous les sites disponibles, à l'exclusion de ceux qui ont été classés avec des preuves de gestion récente (éclaircie commerciale ou coupe à blanc) et où les incendies ou les perturbations d'insectes ont détruit plus de 25% du couvert forestier.

Pour les estimations des taux de croissance et de la durée de vie précoces au niveau des espèces (cf. Fig. 1a ), nous n'avons inclus que les espèces avec un minimum de 30 enregistrements, car une taille d'échantillon plus faible est peu susceptible de fournir de bonnes approximations de la durée de vie des arbres. Cela a abouti à l'inclusion de 110 espèces, avec un échantillon médian de 305 arbres et 12 sites par espèce. Pour évaluer les relations intra-espèces entre la croissance précoce et la durée de vie des arbres, nous avons inclus 82 espèces. En règle générale, nous n'avons inclus que les espèces comptant plus de 150 arbres au total et provenant d'au moins 3 sites. Environ la moitié de nos espèces avaient plus de 300 enregistrements d'arbres (voir Information supplémentaire).

Pour évaluer la taille minimale de l'échantillon nécessaire pour obtenir une estimation représentative de l'âge maximum réel d'une espèce ou d'un site, et pour évaluer comment la taille de l'échantillon affectait les estimations des compromis entre la croissance précoce et la longévité, nous avons rééchantillonné au hasard 500 fois l'échantillon variable. tailles — de 25 à 600 arbres — d'un sous-ensemble de 11 752 arbres Picea mariana provenant de sites NFI-Québec situés au nord de 50,7 ° N. La comparaison des âges maximums de ces sous-ensembles aléatoires d'arbres avec les âges maximums réellement observés montre qu'une taille d'échantillon de 100 arbres donne 99,4% des cas dans des estimations d'âge maximum supérieures au 95e centile de l'ensemble de données d'origine, et dans 67,2% des cas à des âges supérieurs au 99 ^e percentile de l'âge d'origine ( Fig.2a, b). Comme plus de 70% des espèces possédaient au moins 100 arbres, nous avons donc supposé que pour la plupart des espèces, les estimations de leur durée de vie étaient proches de la durée de vie réelle. Nous avons utilisé cette même approche pour évaluer comment la taille de l'échantillon affectait l'estimation des compromis (c.-à-d. L'estimation de la constante de décroissance exponentielle négative; voir la section suivante pour plus de détails). Cette analyse a montré que la taille des échantillons de 300 arbres (correspondant à la taille médiane de l' échantillon pour analyse compromis), conduit à des erreurs moyennes de la pente d' environ 12% (figure supplémentaire. 2c). Ainsi, pour la plupart des espèces, nous obtenons des estimations relativement précises de la force de compromis. De faibles tailles d'échantillons pour certaines espèces entraîneront néanmoins de petites erreurs de la pente moyenne, mais nous nous attendons à ce que les erreurs positives et négatives s'annulent l'une par rapport à l'autre. En effet, nous n'observons pas de biais spécifique de surestimation ou de sous-estimation pour les échantillons de faible taille, car la constante de décroissance exponentielle moyenne pour une taille d'échantillon simulée de 150 arbres est très similaire à celle observée (soit −0,409 contre −0,399) .

Estimations de compromis et évaluation des artefacts possibles

La force des compromis entre la croissance et la durée de vie des arbres a été évaluée pour chaque espèce à l'aide d'une régression quantile de 95 ^e entre le taux de croissance précoce moyen et le logarithme naturel de l'âge en utilisant le package QUANTREG dans R ⁶⁰ , comme

l o g (A (95 t h q u a n t i l e)) = a + b \cdot R W ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ o r L i f e s p a n \approx A (95 t h q u a n t i l e) = e x p (a + b \cdot R W ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯)

(1)

où A est l'âge de l'arbre, est la largeur moyenne de l'anneau au cours des 10 premières années. La constante b décrit la constante de décroissance exponentielle négative (c'est-à-dire le taux exponentiel de diminution de la durée de vie des arbres avec l'augmentation du taux de croissance précoce). Cet ajustement de régression quantile donne des estimations similaires de l'âge maximum des arbres à mesure que le 95e percentile vieillit dans les catégories de taux de croissance précoce groupées (voir les figures supplémentaires 3a – c ). Notez que contrairement au diamètre maximal ne varie fortement entre les arbres lents et à croissance rapide (figure supplémentaire. 3d $\bar{R W}$

). Nous avons choisi une période relativement courte, les dix premières années, pour estimer la croissance précoce, car notre étude incluait certaines espèces à durée de vie relativement courte. Des études antérieures ont trouvé des résultats similaires lors de l'utilisation de périodes plus longues (50 ans) ⁵⁶ , et nous ne prévoyons aucune différence substantielle en utilisant différentes périodes de croissance précoce, car la croissance des arbres est généralement fortement auto-corrélée dans le temps ⁶¹ .

Pour évaluer les forces d'arrêt du commerce au sein des espèces, nous avons calculé la constante de décroissance moyenne ( b , l' équation. 2 ) pour chaque espèce en utilisant l' âge relatif, A / max (A) et la largeur de sonnerie précoce moyenne relative, / max ( ). Le maximum de A et sont des maximums au niveau de l'espèce. Le calcul de la pente moyenne pour toutes les espèces a été pondéré par la racine cubique de la taille de l'échantillon pour tenir compte des grandes différences entre les espèces dans la taille de l'échantillon et la confiance des estimations de compromis. $\bar{R W}$

\bar{R W}

\bar{R W}

Si ces relations suggèrent de véritables compromis, elles peuvent aussi être affectées (ou même motivées par) les approches ou les méthodes analytiques utilisées ici. En particulier, nous évaluons ici l'effet des quatre artefacts possibles suivants sur nos résultats; (1) l'utilisation d'arbres vivants pour estimer la durée de vie des arbres, (2) l'effet des augmentations récentes de la croissance sur la relation précoce-âge de croissance, (3) les effets des décalages de moelle et de la pourriture du bois sur la relation précoce-âge de croissance, (4) d'échantillonnage des artefacts , comme la sélection disproportionnée de grands arbres.

(1)
Utilisation d'arbres vivants: notre analyse comprend principalement des arbres qui ont été échantillonnés lorsqu'ils sont encore vivants, et peuvent donc ne pas être représentatifs de la durée de vie réelle que les arbres peuvent atteindre. Pour évaluer dans quelle mesure l'utilisation d'arbres vivants peut affecter nos résultats, nous analysons et comparons les forces de compromis des arbres morts avant 1900 à des arbres vivants pour 12 espèces avec une disponibilité de données suffisante (minimum de 150 arbres morts et 150 arbres vivants). Comme les pentes des arbres morts et vivants ne diffèrent pas significativement ( Fig.5f , g , coefficient de décroissance exponentielle du test t apparié, t = −0,1095, p = 0,915, n = 12), nous concluons que 95e régressions quantiles sur le vivant les arbres peuvent être utilisés pour estimer la durée de vie des arbres.
(2)
Effet des augmentations récentes de croissance: stimulation récente de la croissance des arbres due par exemple au CO ₂la fertilisation, le réchauffement sous des latitudes plus élevées et / ou les dépôts d'azote peuvent entraîner l'observation d'un compromis. En effet, de récentes augmentations de croissance entraîneront des taux de croissance précoce plus élevés pour les jeunes arbres par rapport aux vieux arbres, ce qui entraînera une relation négative entre la croissance précoce et l'âge des arbres. La comparaison de la force de compromis entre les arbres morts et les arbres vivants fournit des preuves solides que cet effet ne conduit pas au compromis. De plus, nous utilisons une simulation forestière basée sur les données (voir la section «Examen des effets de la stimulation de la croissance sur la dynamique forestière») pour évaluer comment les augmentations de croissance affectent les estimations de la force de compromis. Dans cette simulation, nous avons utilisé les données réelles des cernes pour simuler des augmentations de croissance réalistes de Picea marianatrajectoires des cernes en réponse au réchauffement des hautes latitudes. En échantillonnant de ces trajectoires à la fin de la période d'augmentation de la croissance (c. -à- année 350), et dans une période sans augmentation de croissance récentes (c. -à- année 600, voir la figure. 3e ), nous établissons que la croissance augmente le résultat que dans un petite surestimation du compromis, diminuant le coefficient de décroissance exponentielle de −0,37 à −0,44 (voir Fig. 9c supplémentaire ). Ainsi, il est peu probable que la stimulation récente de la croissance soit à l'origine de la relation négative entre la croissance précoce et la durée de vie des arbres.
(3)
Décalage de la moelle: les données des anneaux d'arbre, en particulier celles acquises à partir de l'ITRDB, peuvent manquer les sections les plus internes en raison de noyaux incomplets, de centres pourris ou d'un alignement imparfait du foreur d'incrément. L'absence d'anneaux entraînera une sous-estimation de l'âge des arbres et une estimation inexacte des taux de croissance précoce et pourrait donc affecter la relation estimée entre la croissance précoce et la durée de vie. Cependant, la largeur des anneaux dans la plupart des espèces diminue avec l'âge et la taille des arbres ¹⁷, et même les arbres affichant une production de bois constante avec l'âge montreront une largeur d'anneau décroissante en raison de la géométrie. Ainsi, une croissance précoce de ces échantillons sous-estimera les taux de croissance réels et affaiblirait très probablement le compromis observé, plutôt que de le renforcer. Une comparaison des espèces présentes à la fois dans les ensembles de données NFI-Québec et ITRDB le confirme. L'ensemble de données NFI-Québec a été moins touché par les problèmes de décalage de la moelle, car les arbres ont été soigneusement criblés et les arbres présentant des différences substantielles entre les largeurs de cernes cumulatives et les diamètres de champ ont été exclus. Pourtant, nous constatons que les pentes étaient plus négatives pour NFI-Québec que pour l'ITRDB (moyenne b de −0,25 pour le Québec vs −0,10 pour l'ITRDB, test t.t.parié bilatéral, t = 2,49, p = 0,047, n = 7 espèces) et les décalages de moelle n'expliquent donc pas la relation. Cette comparaison montre également que les estimations de la force des compromis entre la croissance précoce et la longévité déduites des données de l'ITRDB sont probablement prudentes, car les données du Québec peuvent être considérées comme de meilleure qualité et ont été recueillies selon des protocoles standards. En revanche, les données de l'ITRDB peuvent contenir des séries incomplètes et ont été collectées à des fins inconnues, et ces problèmes affaiblissent probablement les compromis dans l'ITRDB.
(4)
Biais d'échantillonnage: un biais potentiel dans notre ensemble de données peut survenir en raison de la tendance des études sur les cernes à échantillonner principalement les grands arbres sur le terrain (c.-à-d. Biais de sélection des grands arbres ^{62 , 63 , 64} ). Cela peut entraîner une relation négative entre la croissance précoce et l'âge des arbres, car les jeunes arbres à croissance lente ont tendance à être sous-représentés dans l'échantillon de cernes (c'est-à-dire qu'ils n'ont pas encore atteint le seuil de taille minimale du champ), par rapport aux jeunes à croissance rapide. des arbres beaucoup plus gros et donc plus susceptibles d'être échantillonnés. Cet effet réduirait le nombre d'arbres à croissance précoce lente et jeunes âges dans l'échantillon de cernes (c'est-à-dire les arbres dans le coin inférieur gauche des graphiques de croissance précoce-durée de vie, cf. Fig. 6a supplémentaire ), et entraîne une surestimation des estimations d'âge au 95 ^e centile pour les arbres à croissance lente. Notre approche pour estimer dans quelle mesure ce biais a affecté nos estimations des compromis entre la croissance et la durée de vie était la suivante. Nous avons d'abord utilisé les données NFI-Québec sur les cernes de Picea mariana , combinées aux données des parcelles du Québec pour reconstruire un nouvel ensemble de données artificielles sur les cernes avec une distribution de fréquence de taille identique à la distribution de fréquence de taille de population pour cette espèce au Québec (Fig. . 6b ). Pour chaque arbre de Picea marianaéchantillonnés pour leurs cernes, nous connaissons le taux de croissance précoce et l'âge, ainsi que la trajectoire complète du diamètre et de l'âge jusqu'à l'année d'échantillonnage. À partir de ces données, nous avons rééchantillonné pour chaque classe de taille (en largeurs de bacs de 2 cm) le même nombre d'arbres que celui observé sur le terrain. En faisant cela, nous avons rempli les données manquantes des arbres de moins de 91 mm et avons créé un nouvel ensemble de données artificielles sur les anneaux d'arbres qui avaient une structure de taille identique à celle observée sur le terrain. Nous connaissons le taux de croissance moyen au cours des dix premières années et l'âge auquel chaque arbre a atteint le diamètre de sa classe de taille respective, et pourrions ainsi reconstruire les graphiques du taux de croissance précoce en fonction de l'âge des arbres pour l'ensemble de la population, y compris les classes de taille plus petites. qui manquaient dans notre échantillon original de cernes.Nous avons ensuite comparé la relation entre la croissance précoce et la durée de vie de la population complète à celle des arbres de plus de 91 mm, imitant le protocole de collecte sur le terrain NFI-Québec. Cela montre que la diminution exponentielle est légèrement plus grande (b = -0,505 -0,470 par rapport à des arbres> 91 mm) et que l'ordonnée à l' origine est plus faible (159 à 220 ans , par rapport à des arbres> 91 mm) lors de l' échantillonnage de tous les arbres par rapport aux seuls arbres ayant des diamètres> 91 mm (Fig supplémentaire. 6 ). Ainsi, l'utilisation d'un seuil de taille minimale (91 mm) dans l'IFN du Québec entraîne une légère sous-estimation du compromis (d'environ 7%) pour l' ensemble de données Picea mariana . Nous avons également rééchantillonné à partir de cet ensemble de données artificielles les 10% plus grands arbres, pour imiter un scénario d'échantillonnage hypothétique de cernes standard qui n'échantillonne que les plus grands arbres. Un tel scénario d'échantillonnage a abouti à une constante de décroissance de −0,432, entraînant à nouveau une légère sous-estimation du véritable compromis. Cette simulation prouve que le compromis n'est pas le résultat d'un biais d'échantillonnage.

Facteurs environnementaux possibles des compromis

Nous avons évalué si le compromis observé entre la croissance précoce et la durée de vie des arbres pouvait être causé par la covariance de la croissance et de la durée de vie avec le climat, le sol ou la concurrence. La variation de température, par exemple, réduit la croissance des arbres et la durée de vie de diverses espèces (cf. Fig. 2a, b ). À cette fin, nous avons calculé les taux de croissance précoce moyens au niveau du site et l'âge maximal des arbres pour un ensemble d'espèces couvrant différentes régions géographiques (Amérique du Nord, Europe et Québec). Pour le Québec, nous avons combiné plusieurs emplacements à proximité pour obtenir un minimum de 30 arbres par site, car la taille des échantillons était faible pour chaque emplacement. La température annuelle moyenne et les précipitations au niveau du site ont été obtenues à partir de WorldClim ⁶⁵. Nous avons ensuite évalué, pour neuf espèces différentes, l'effet de la température et des précipitations sur la croissance moyenne au début de la vie au niveau du site et l'âge maximum des arbres en utilisant la régression sur l'axe principal du package smart-3 ⁶⁶ . Ces analyses confirment que la croissance au début de la vie est positivement liée à la température pour les neuf espèces étudiées, et que la durée de vie diminue significativement avec la température pour sept des neuf espèces (voir Fig. 2a, b ). Utilisation de modèles linéaires à effets mixtes avec des espèces comme facteur aléatoire (nlme-package-R ⁶⁷), nous constatons que pour les neuf espèces, la croissance moyenne au début de la vie augmente en moyenne de 0,11 mm pour chaque degré d'augmentation de température, tandis que la durée de vie diminue de 13 ans pour chaque degré d'augmentation de température. Les précipitations n'ont pas d'effet significatif sur la croissance au début de la vie ou la durée de vie des arbres.

Pour déterminer si la diminution de la durée de vie est un effet direct de l'augmentation de la température ou de l'augmentation de la croissance au début de la vie, des modèles à effets mixtes ont été exécutés pour les neuf espèces qui incluaient simultanément la température et le taux de croissance moyen au début de la vie comme variables explicatives de la variation de la durée de vie des arbres. Pour tenir compte des différences d'espèces en termes de croissance et d'âge, nous avons utilisé la largeur moyenne relative des premiers anneaux ( / max ( )) et l'âge maximal relatif ( A / max (A) ), et utilisé des espèces comme facteur aléatoire avec des interceptions aléatoires pour la croissance et la température au début de la vie. Cette analyse montre que la croissance moyenne au début de la vie est un meilleur prédicteur de la durée de vie des arbres que la température ( t $\bar{R W}$

\bar{R W}

-valeur croissance précoce = −7,2, p <0,001, t -valeur température = −2,5, p = 0,012). Une analyse similaire pour Picea mariana seule confirme que le principal moteur de la durée de vie est le taux de croissance moyen au début de la vie et non la température ou d'autres variables environnementales. Par exemple, l'analyse de la croissance au début de la vie par rapport à la durée de vie dans différentes classes de température (de 2 ° C) reste forte, tandis que la relation entre la température et la durée de vie se décompose lorsqu'elle est analysée en classes de taux de croissance ( Fig.2d ). De même, les compromis restent forts pour Picea marianamême lors de l'analyse des données dans les classes de couverture de la couronne (c'est-à-dire une indication de la compétition au niveau du peuplement), ou lors de l'analyse des données dans différentes classes de sol (Fig. 8 supplémentaire ).

Examen des effets de la stimulation de la croissance sur la dynamique forestière

Nous examinons l'effet du compromis observé entre la longévité de la croissance sur la dynamique des forêts (croissance, mortalité et stocks sur pied) pour une stimulation de la croissance réaliste, comme prévu par les changements de température. Pour ce faire, nous utilisons une approche de simulation forestière axée sur les données dans laquelle nous utilisons des données observées sur les cernes et des estimations réalistes des taux de mortalité liés à la taille qui se traduisent par un compromis entre la croissance précoce et la durée de vie très similaire au compromis observé. La stimulation de la croissance des arbres a été estimée à l'aide de la sensibilité à la température des données de cernes provenant du grand gradient de température pour le Québec (cf. Fig. 7 supplémentaire ). L'approche complète est décrite ci-dessous.

Comme le démontre notre manuscrit principal, les données sur les cernes du Québec révèlent un compromis entre la croissance et la longévité des arbres, qui peut être médiée par une augmentation rapide de la mortalité avec un diamètre croissant. Il existe non seulement des carottes d'arbres, mais également des données détaillées de recensement forestier pour cette région, permettant de reconstruire les relations de mortalité dépendant de la taille. Cette analyse a été effectuée en utilisant uniquement les données des inventaires forestiers du Québec au nord de 50,7 ° N. Premièrement, nous estimons la mortalité, μ, en fonction du diamètre des arbres en utilisant à la fois les inventaires de données de recensement forestier et les enregistrements de cernes individuels de Picea mariana de NFI-Québec. Nous supposons un état stationnaire de la distribution des nombres de diamètre de l'arbre ( D ), N (D) . Ainsi, pour une classe de diamètre avec D dans l'intervalle [D, D + δD ]

0 = d N ( D ) d t = I (D) - L (D) - μ \cdot (D) .

(2)

Ici I (D) est le nombre d'individus grandissant dans la classe de diamètre [ D, D + δD ] par unité de temps, et de même L (D) le nombre d'individus quittant la même classe de diamètre par unité de temps. Ainsi, la mortalité peut être estimée à partir de la distribution du diamètre constant, obtenu à partir de données de tracé (figure supplémentaire. 7b ), et le nombre d'en-producteurs et sortants, estimés à partir de la distribution des diamètres et des ensembles de trajectoires de croissance choisis au hasard, comme

μ (D) = I ( D ) - L ( D ) N ( D ) .

(3)

Le résultat est montré sur la figure 3a , avec un modèle polynomial du quatrième ordre de la forme

μ (D) = {0 b + k \cdot (D - D 0) 4 f o r D \leq D 0 f o r D > D 0 .

(4)

Ici b = 0,025, k = 3 × 10 ⁻¹¹ et D ₀ = 91 mm, qui est le diamètre minimal d'échantillonnage utilisé pour l'IFN-Québec. La justification pour fixer la mortalité en dessous de D ₀ à zéro dans ce modèle est que les arbres échantillonnés pour les cernes ont tous survécu à ce diamètre (car seuls les arbres d'un diamètre> 91 mm ont été carottés). Ainsi, seule la mise à zéro de la mortalité pour les arbres <91 mm permet une comparaison correcte des résultats de simulation avec les données observées. Nous avons fini par utiliser ce modèle car il reproduisait assez bien le compromis observé entre croissance et longévité (voir Fig. 3b). La force du compromis simulé est robuste en ce qui concerne le choix de la fonction de mortalité, car des taux de mortalité en augmentation linéaire reproduisent également le compromis observé. L'augmentation des taux de mortalité vers des classes de taille plus grandes est cohérente avec les observations de mortalité en fonction de la taille dans les arbres tempérés et tropicaux ^{35 , 36 , 40 , 68} , et soutient la notion de seuil de taille maximale spécifique à l'espèce ⁶⁴ . Pour Picea mariana , la taille maximale des arbres au 99e percentile est de 353 mm, proche des diamètres auxquels on constate de fortes augmentations de la mortalité des arbres (cf. Fig. 3a). À des fins de comparaison, nous avons également calculé un taux de mortalité en fonction de l'âge et effectué des simulations alternatives à l'aide de ce modèle de mortalité. La relation de mortalité dépendante de l'âge a été dérivée d'une manière similaire à la courbe de mortalité par taille en répétant la procédure et les calculs ci-dessus (équations 2 et 3 ) pour les classes d'âge (annuelles). La mortalité dépendante de l'âge a été paramétrée comme suit:

μ (A) = {0 a + b * A f o r A \leq A 0 f o r A > A 0,

(5)

avec a = 0,021 et b = 0,0000015. De manière analogue au modèle de mortalité dépendant du diamètre, nous avons fixé la mortalité à zéro pour les arbres de moins de 74 ans ( A ₀ ), qui est l'âge auquel l' arbre moyen de Picea mariana atteint 91 mm de diamètre ( D ₀ ).

Nous avons ensuite créé une séquence de 600 ans de cohortes d'arbres ensemencés annuellement, 1250 membres. Chaque membre d'une cohorte est une trajectoire de croissance du diamètre des arbres choisie au hasard, dérivée des noyaux des cernes, prolongée dans le temps jusqu'à un âge de 500 ans. Les courtes trajectoires de croissance ont été prolongées en utilisant la croissance moyenne des 10 arbres les plus anciens qui avaient une largeur d'anneau similaire au cours des dix premières années de croissance. À cette fin, toute la largeur moyenne des premiers anneaux a été regroupée en six classes de largeur des anneaux précoces égales.

Tous les arbres de cette cohorte d'arbres ainsi construite vivent, par construction, exactement 600 ans. Des structures d'âge réalistes ont été réalisées en attribuant séquentiellement (année après année et arbre par arbre) la mort aux arbres où un générateur de nombres aléatoires a identifié les individus plus petits que μ (D) ou μ (A) . Pour tester le réalisme de cette procédure, nous avons comparé l'âge des arbres prédit et observé par rapport à la relation de largeur de l'anneau précoce - ou c'est-à-dire le compromis croissance-longévité. La pente de la relation pour le modèle de mortalité en fonction de la diamètre μ (D) est très proche observé (Fig supplémentaire. 9a), et constitue donc une représentation réaliste du processus de mortalité observé et justifie son utilisation pour examiner l'effet d'une stimulation de la croissance sur les stocks sur pied. En revanche, nous constatons que le modèle de mortalité liée à l' âge μ (A) n'a pas abouti à une durée de vie de l' arbre et le commerce entre la croissance précoce significative (supplémentaire Fig. 9b ), fournissant une comparaison idéale pour les modèles qui n'incorporer la observée compromis.

Pour imiter la stimulation de la croissance, nous avons stimulé la croissance des trajectoires à partir de l'année t ₀ = 300 ans à partir de la séquence de 600 ans de cohortes, tout en exposant les trajectoires sur toute la période de 600 ans à l'algorithme de mortalité qui vient d'être décrit. Nous avons stimulé le taux de croissance, (mm an ⁻¹ ) à partir de l'année t ₀ = 300 ans selon $\bar{R W}$

R W s t i m ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ (t) = R W ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ (t) \cdot exp (λ (A) \cdot δ T (t)),

(6)

δ T (t) = {d T ¯ ¯ ¯ ¯ ¯ ¯ ¯ d t \cdot (t - t 0), c o n s t, t - t 0 < τ t - t 0 \geq τ

(7)

où δT (t) est une tendance de température normalisée (année ⁻¹ ), λ (A) une fonction sans unité de l'âge de l'arbre représentant que la sensibilité de croissance des arbres jeunes et vieux à la température peut varier avec l'âge de ⁵⁹ ans , et τ est de 50 ans, la durée de la période de stimulation de la croissance. Nous avons calculé la tendance de température observée pour le Québec au cours des 100 dernières années à partir des données du CRUTEMP ⁶⁹ , et avons simulé des augmentations de croissance de 300 à 350 en réponse au taux de réchauffement observé, estimé à 0,0221 ° C par an ^-1 . Nous avons utilisé une approche de substitution spatio-temporelle sur l'ensemble de données du Québec ⁴³ pour estimer la réponse de largeur d'anneau de Picea marianaà la température. Nous avons effectué ces simulations dans des tranches d'âge de 10 ans (0–10, 10–20,…. 140–150,> 150 ans) car les jeunes arbres sont plus sensibles aux augmentations de température que les arbres plus âgés (Fig. 9d supplémentaire ), et utiliser un modèle exponentiel de la forme

R W ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ (A, T) = a \cdot e x p (λ (A) \cdot δ T),

(8)

où a est une constante, λ (A) est le taux d'accroissement exponentiel pour la classe d'âge [A, A + δA] et δT = (T - 0) (° C). Nous avons ensuite utilisé l'augmentation exponentielle de la croissance avec la température pour chaque tranche d'âge, λ (A) , pour estimer la relation entre l'âge de l'arbre et λ (A) (figure 9e supplémentaire ). Dans tous les cas, la modulation de l'âge du stimulus est

λ (A) = {0.0000132 \cdot A 2 - 0.00291 \cdot A + 0.229, 0.07, A < 135 A \geq 135 .

(9)

Enfin, nous avons comparé l'effet de la stimulation de la croissance sur la dynamique des forêts à la simulation sans augmentation de la croissance (référence) pour les deux modèles de mortalité différents. Nous avons également effectué une simulation où nous avons multiplié la série de croissance complète par 2, comme une représentation de l'effet de la stimulation de la croissance sur une espèce à croissance plus rapide. Enfin, nous avons évalué pour chaque simulation la croissance moyenne de la largeur des anneaux, le taux de mortalité des tiges, l'âge des plus gros arbres (75e centile) morts et la variation du stock total de la surface terrière au fil du temps pour l'ensemble de la population. Pour la mortalité de la tige et les stocks de surface de base, nous calculons et présentons l'évolution de la dynamique du scénario de stimulation de la croissance par rapport au scénario de référence sans stimulation de la croissance. Toutes les analyses et simulations ont été réalisées à l'aide de R-studio, version 0.99.903⁷⁰ . Les cartes en chiffres SI ont été produites à l'aide de la fonction ggmap du package R 'ggplot2'⁷¹

Disponibilité des données

Toutes les métadonnées et les données sur la croissance précoce et l'âge des arbres sont disponibles sur https://doi.org/10.6084/m9.figshare.12620414 .

Disponibilité du code

Le code source pour reproduire la figure 1 est disponible sur https://doi.org/10.6084/m9.figshare.12620414 . Les codes supplémentaires utilisés dans cette analyse sont disponibles auprès de l'auteur correspondant sur demande raisonnable.

Références

1.
Ballantyne, AP, Alden, CB, Miller, JB, Tans, PP & White, JWC Augmentation de l'absorption nette de dioxyde de carbone observée par les terres et les océans au cours des 50 dernières années. Nature 488 , 70–72 (2012).
LES PUBLICITÉS CAS PubMed Google Scholar
2.
Pan, Y. et coll. Un puits de carbone important et persistant dans les forêts du monde. Science 333 , 988–993 (2011).
LES PUBLICITÉS CAS PubMed Google Scholar
3.
Pugh, TA et coll. Rôle de la repousse des forêts dans la dynamique mondiale des puits de carbone. Proc. Natl Acad. Sci. USA 116 , 4382–4387 (2019).
LES PUBLICITÉS CAS PubMed Google Scholar
4.
Brienen, R. et coll. Déclin à long terme du puits de carbone amazonien. Nature 519 , 344–348 (2015).
LES PUBLICITÉS CAS PubMed Google Scholar
5.
Sitch, S. et coll. Évaluation du cycle du carbone terrestre, de la géographie future des plantes et des rétroactions du cycle climat-carbone à l'aide de cinq modèles dynamiques de végétation globale (DGVM). Glob. Changer Biol. 14 , 2015-2039 (2008).
LES PUBLICITÉS Google Scholar
6.
Cox, PM Contraintes émergentes sur les rétroactions climat-cycle du carbone. Curr. Clim. Changement Rep. 5 , 275-281 (2019).
PubMed PubMed Central Google Scholar
7.
Manusch, C., Bugmann, H., Heiri, C. & Wolf, A. Mortalité des arbres dans les modèles de végétation dynamique - une caractéristique clé pour simuler avec précision les propriétés forestières. Ecol. Modèle. 243 , 101-111 (2012).
Google Scholar
8.
Friend, AD et al. Le temps de séjour du carbone domine l'incertitude dans les réponses de la végétation terrestre au climat futur et au CO ₂ atmosphérique . Proc. Natl Acad.Sci. ETATS-UNIS. https://doi.org/10.1073/pnas.1222477110 (2013).
9.
Bugmann, H. & Bigler, C. L' effet de fertilisation au CO ₂ dans les forêts sera-t-il compensé par une réduction de la longévité des arbres? Oecologia 165 , 533-544 (2011).
LES PUBLICITÉS PubMed Google Scholar
dix.
Körner, C. Une question de longévité des arbres. Science 355 , 130–131 (2017).
LES PUBLICITÉS PubMed Google Scholar
11.
Fisher, RA et coll. Démographie de la végétation dans les modèles du système terrestre: examen des progrès et des priorités. Glob. Changer Biol. 24 , 35–54 (2018).
LES PUBLICITÉS Google Scholar
12.
Searle, EB & Chen, HY Déclin temporel de la longévité des arbres associé à des taux de croissance à vie plus rapides dans les forêts boréales. Environ. Res. Lett. 13 , 125003 (2018).
LES PUBLICITÉS CAS Google Scholar
13.
Loehle, C. Stratégies d'histoire de vie des arbres - le rôle des défenses. Pouvez. J. Pour. Res. 18 , 209-222 (1988).
Google Scholar
14.
Schulman, E. Longévité sous l'adversité chez les conifères. Science 119 , 396–399 (1954).
LES PUBLICITÉS CAS PubMed Google Scholar
15.
Wright, SJ et coll. Traits fonctionnels et compromis croissance-mortalité chez les arbres tropicaux. Ecology 91 , 3664–3674 (2011).
Google Scholar
16.
Bazzaz, F. L'écologie physiologique de la succession végétale. Annu. Rev. Ecol. Syst. 10 , 351 à 371 (1979).
Google Scholar
17.
Black, BA, Colbert, JJ et Pederson, N. Relations entre les taux de croissance radiale et la durée de vie des espèces d'arbres nord-américaines. Ecoscience 15 , 349–357 (2008).
Google Scholar
18.
Johnson, SE & Abrams, MD Relations entre les classes d'âge, la longévité et le taux de croissance: accroissement prolongé de la croissance chez les vieux arbres de l'est des États-Unis. Tree Physiol. 29 , 1317–1328 (2009).
PubMed Google Scholar
19.
Bigler, C. & Veblen, TT Des taux de croissance précoce accrus réduisent la longévité des conifères dans les forêts subalpines. Oikos 118 , 1130-1138 (2009).
Google Scholar
20.
Di Filippo, A. et coll. La longévité des feuillus feuillus à feuilles caduques dans les forêts tempérées de l'hémisphère nord: aperçus des séries de cernes. De face. Ecol. Évolution 3 , 46 (2015).
Google Scholar
21.
Büntgen, U. et coll. Capacité limitée de croissance des arbres à atténuer l'effet de serre global sous le réchauffement prévu. Nat. Commun. 10 , 2171 (2019).
LES PUBLICITÉS PubMed PubMed Central Google Scholar
22.
Cailleret, M. et coll. Une synthèse des schémas de croissance radiale précédant la mortalité des arbres. Glob. Changer Biol. 23 , 1675–1690 (2017).
LES PUBLICITÉS Google Scholar
23.
Irlande, KB, Moore, MM, Fulé, PZ, Zegler, TJ & Keane, RE Une croissance lente tout au long de la vie prédispose les arbres de Populus tremuloides à la mortalité. Oecologia 175 , 847–859 (2014).
LES PUBLICITÉS PubMed Google Scholar
24.
Wyckoff, PH & Clark, JS La relation entre la croissance et la mortalité pour sept espèces d'arbres concomitantes dans le sud des Appalaches. J. Ecol. 90 , 604–615 (2002).
Google Scholar
25.
Rogers, BM et coll. Détection des signaux d'alerte précoce de la mortalité des arbres en Amérique du Nord boréale à l'aide de données satellitaires multi-échelles. Glob. Changer Biol. 24 , 2284-2304 (2018).
LES PUBLICITÉS Google Scholar
26.
Schöngart, J., Piedade, MTF, Wittmann, F., Junk, WJ & Worbes, M. Modèles de croissance du bois de Macrolobium acaciifolium (Benth.) Benth. (Fabaceae) dans les forêts des plaines inondables d'Amazonie d'eau noire et d'eau vive. Oecologia 145 , 454–461 (2005).
LES PUBLICITÉS PubMed Google Scholar
27.
Brienen, RJW, Zuidema, PA & Martinez-Ramos, MM Atteindre la canopée dans les forêts tropicales sèches et humides: de fortes différences dans les trajectoires de croissance des arbres reflètent la variation des conditions de croissance. Oecologia 163 , 485–496 (2010).
LES PUBLICITÉS PubMed Google Scholar
28.
Speakman, J. Taille corporelle, métabolisme énergétique et durée de vie. J. Exp. Biol. 208 , 1717–1730 (2005).
PubMed Google Scholar
29.
Issartel, J. & Coiffard, C. Longévité extrême dans les arbres: vivre lentement, mourir vieux? Oecologia 165 , 1–5 (2011).
LES PUBLICITÉS PubMed Google Scholar
30.
Mencuccini, M. et coll. Le vieillissement induit par la taille réduit la vigueur des arbres. Ecol. Lett. 8 , 1183-1190 (2005).
CAS PubMed Google Scholar
31.
Lanner, R. & Connor, KF La sénescence du pin bristlecone? Exp. Gerontol. 36 , 675 à 685 (2001).
CAS PubMed Google Scholar
32.
Siefert, A. et coll. Une méta ‐ analyse globale de l'étendue relative de la variation intraspécifique des caractères dans les communautés végétales. Ecol. Lett. 18 , 1406–1419 (2015).
PubMed Google Scholar
33.
de la Mata, R., Hood, S. & Sala, A. L'épidémie d'insectes déplace la direction de la sélection des taux de croissance rapides vers les taux de croissance lents chez le conifère longévif Pinus ponderosa. Proc. Natl Acad. Sci. USA 114 , 7391–7396 (2017).
PubMed Google Scholar
34.
Roskilly, B., Keeling, E., Hood, S., Giuggiola, A. & Sala, A. Les effets fonctionnels contradictoires de la structure de la fosse de xylème sont liés au compromis croissance-longévité chez une espèce de conifère. Proc. Natl Acad. Sci. USA . https://doi.org/10.1073/pnas.1900734116 (2019).
35.
Hurst, JM, Allen, RB, Coomes, DA et Duncan, RP La mortalité des arbres selon la taille varie selon le surpeuplement du quartier et les perturbations dans une forêt montagnarde de Nothofagus. PLoS ONE 6 , e26670 à e26670 (2011).
LES PUBLICITÉS CAS PubMed PubMed Central Google Scholar
36.
Johnson, DJ et coll. Survie dépendante de la taille et sensible au climat dans les arbres tropicaux. Nat. Ecol. Evol. 2 , 1436 (2018).
PubMed Google Scholar
37.
Thomas, SC Hauteur asymptotique comme prédicteur de la croissance et des caractéristiques allométriques des arbres de la forêt tropicale malaisienne (vol 83, pg 556, 1996). Un m. J. Bot. 83 , 1570-1570 (1996).
Google Scholar
38.
Ryan, MG & Yoder, BJ Limites hydrauliques à la hauteur et à la croissance des arbres. Bioscience 47 , 235–242 (1997).
Google Scholar
39.
Koch, GW, Sillett, SC, Jennings, GM & Davis, SD Les limites de la hauteur des arbres. Nature 428 , 851–854 (2004).
LES PUBLICITÉS CAS PubMed Google Scholar
40.
Stovall, AE, Shugart, H. & Yang, X. La hauteur des arbres explique le risque de mortalité lors d'une sécheresse intense. Nat. Commun. 10 , 1-6 (2019).
Google Scholar
41.
Pfeifer, EM, Hicke, JA & Meddens, AJ Observations et modélisation des stocks et des flux de carbone des arbres aériens suite à une épidémie de scolytes dans l'ouest des États-Unis. Glob. Changer Biol. 17 , 339–350 (2011).
LES PUBLICITÉS Google Scholar
42.
Wu, C. et coll. Accélération de l'amélioration de la croissance des forêts en raison des changements climatiques et atmosphériques en Colombie-Britannique, au Canada, de 1956 à 2001. Sci. Rep. 4 , 4461 (2014).
PubMed PubMed Central Google Scholar
43.
Huang, J.-G. et coll. Impact du climat futur sur la croissance radiale de quatre principales espèces d'arbres boréales dans l'est de la forêt boréale canadienne. PLoS ONE 8 , e56758 (2013).
LES PUBLICITÉS CAS PubMed PubMed Central Google Scholar
44.
McDowell, NG et Allen, CD La loi de Darcy prédit une mortalité forestière généralisée sous le réchauffement climatique. Nat. Clim. Changement 5 , 669 (2015).
LES PUBLICITÉS Google Scholar
45.
Kubiske, ME, Woodall, CW & Kern, CC Augmentation du développement des peuplements à concentration de CO2 atmosphérique dans les forêts de peupliers faux-trembles: les directives de gestion de la densité désuètes doivent-elles être révisées pour toutes les espèces? J. Pour. 117 , 38–45 (2018).
Google Scholar
46.
Pretzsch, H., Biber, P., Schütze, G., Uhl, E. & Rötzer, T. La dynamique de croissance des peuplements forestiers en Europe centrale s'est accélérée depuis 1870. Nat. Commun. 5 , 4967 (2014).
LES PUBLICITÉS CAS PubMed PubMed Central Google Scholar
47.
Duchesne, L., Houle, D., Ouimet, R., Lambert, M.-C. & Logan, T. Carbone aérien dans les forêts du Québec: quantification des stocks à l'échelle provinciale et évaluation des effets de la température, des précipitations et des propriétés édaphiques sur le peuplement potentiel. PeerJ 4 , e1767 à e1767 (2016).
PubMed PubMed Central Google Scholar
48.
Needham, JF, Chambers, J., Fisher, R., Knox, R. & Koven, CD Réponses de la forêt au CO2 élevé simulé sous d'autres hypothèses de mortalité en fonction de la taille et de l'âge. Glob. Changer Biol . https://doi.org/10.1111/gcb.15254 (2020).
49.
Allen, CD et coll. Une vue d'ensemble de la mortalité des arbres due à la sécheresse et à la chaleur révèle les risques émergents de changement climatique pour les forêts. Ecol. Manag. 259 , 660-684 (2010).
Google Scholar
50.
Yu, K. et coll. Diminution généralisée du temps de renouvellement du carbone de la végétation vivante dans les zones climatiques forestières. Proc. Natl Acad. Sci. USA 116 , 24662–24667 (2019).
51.
Peng, C. et coll. Une augmentation généralisée de la mortalité des arbres causée par la sécheresse dans les forêts boréales du Canada. Nat. Clim. changement 1 , 467 (2011).
LES PUBLICITÉS Google Scholar
52.
MFFP. Ministère des Forêts de la Faune et des Parcs. Norme d′inventaire écoforestier, Placettes-échantillons temporaires, Édition 2016. https://www.mffp.gouv.qc.ca/publications/forets/connaissances/Norme-PET.pdf. (2016).
53.
Duchesne, L., D'Orangeville, L., Ouimet, R., Houle, D. & Kneeshaw, D. Extraction de signaux climatiques cohérents des cernes à travers les échelles spatiales à partir de données d'inventaire forestier étendues. PloS ONE 12 , e0189444 (2017).
PubMed PubMed Central Google Scholar
54.
Locosselli, GM, Krottenthaler, S., Pitsch, P., Anhuf, D. & Ceccantini, G. Âge et taux de croissance des espèces d'arbres congénères (Hymenaea spp. – Leguminosae) Habitant différents biomes tropicaux. Erdkunde 71 , 45-57 (2017).
Google Scholar
55.
López, L., Rodríguez-Catón, M. & Villalba, R. Convergence des réponses de croissance des arbres tropicaux au climat induit par le stress hydrique. Ecography 42 , 1899-1912 (2019).
56.
Bigler, C. Compromis entre le taux de croissance, la taille des arbres et la durée de vie du pin de montagne (Pinus montana) dans le parc national suisse. PloS one 11 , e0150402 (2016).
PubMed PubMed Central Google Scholar
57.
Helama, S., Lindholm, M., Timonen, M. & Eronen, M. Modifications dendrochronologiques de la limite du pin dans l'extrême nord de la Finlande au cours des 7,5 derniers millénaires. Boreas 33 , 250–259 (2004).
Google Scholar
58.
Grudd, H. et coll. Une chronologie des cernes de 7400 ans dans le nord de la Laponie suédoise: variabilité climatique naturelle exprimée sur des échelles de temps annuelles à millénaires. Holocene 12 , 657–665 (2002).
LES PUBLICITÉS Google Scholar
59.
Voelker, SL dans Changements liés à la taille et à l'âge dans la structure et la fonction des arbres, 455–479 (Springer, 2011).
60.
Koenker, R. quantreg: régression quantile. Version du package R 5.05. (R Foundation for Statistical Computing, Vienne, 2013) http://CRAN.R-project.org/package=quantreg .
61.
Brienen, RJW, Zuidema, PA & Pendant, HJ Croissance autocorrélée des arbres des forêts tropicales: élucidation des modèles et quantification des conséquences. Ecol. Manag. 237 , 179-190 (2006).
Google Scholar
62.
Brienen, RJW, Gloor, E. & Zuidema, PA Détecter les preuves de la fertilisation au CO _{2 à} partir des études de cernes : le rôle potentiel des biais d'échantillonnage. Glob. Biogéochem. Cycles 26 , GB1025 (2012).
LES PUBLICITÉS Google Scholar
63.
Nehrbass-Ahles, C. et al. L'influence du plan d'échantillonnage sur la quantification de la croissance forestière basée sur les cernes. Glob. Changer Biol. 20 , 2867-2885 (2014).
LES PUBLICITÉS Google Scholar
64.
Duchesne, L. et al. Les fortes augmentations de croissance apparentes dans les forêts boréales, déduites des cernes, sont un artefact de biais d'échantillonnage. Sci. Rep. 9 , 6832 (2019).
LES PUBLICITÉS PubMed PubMed Central Google Scholar
65.
Hijmans, RJ, Cameron, SE, Parra, JL, Jones, PG & Jarvis, A. Surfaces climatiques interpolées à très haute résolution pour les zones terrestres mondiales. Int. J. Climatol. 25 , 1965-1978 (2005).
Google Scholar
66.
Warton, DI, Duursma, RA, Falster, DS & Taskinen, S. smatr 3-an R package pour l'estimation et l'inférence sur les lignes allométriques. Méthodes Ecol. Evol. 3 , 257–259 (2012).
Google Scholar
67.
Pinheiro, J., Bates, D., DebRoy, S. & Sarkar, D. Modèles d'effets mixtes linéaires et non linéaires. Paquet R Vers. 3 , 57 (2007).
Google Scholar
68.
Caspersen, JP, Vanderwel, MC, Cole, WG & Purves, DW Comment la productivité des peuplements résulte de la croissance et de la mortalité dépendant de la taille et de la concurrence. PloS ONE 6 , e28660 (2011).
LES PUBLICITÉS CAS PubMed PubMed Central Google Scholar
69.
Jones, PD & Moberg, A. Variations hémisphériques et à grande échelle de la température de l'air à la surface: une révision approfondie et une mise à jour jusqu'en 2001. J. Clim. 16 , 206-223 (2003).
LES PUBLICITÉS Google Scholar
70.
R_Core_Team. R: Un langage et un environnement pour le calcul statistique. (2013).
71.
Wickham, H. ggplot2: graphiques élégants pour l'analyse des données . (Springer, 2016).

Télécharger les références

Remerciements

Nous remercions les contributeurs de la Banque internationale de données sur les cernes pour avoir mis à disposition les données brutes sur les cernes utilisées dans cette étude, et remercions le personnel de la Direction des inventaires forestiers du ministère des Forêts, de la Faune et des Parcs du Québec pour le partage de données sur les cernes et les parcelles d'échantillonnage du programme d'inventaire forestier au Québec, Canada. RJWB a été soutenu par la subvention NERC NE / S008659 / 1, EG a été soutenu par la subvention NERC NE / N012542 / 1, et GL et GC ont été soutenus par les subventions FAPESP 12 / 50457-4 et 17 / 5008-3, JB a été soutenu par le Centre National de la Recherche Scientifique (CNRS) de France à travers le programme présidentiel Make Our Planet Great Again. SH a été soutenu par l'Académie de Finlande, et l'ADF a été soutenu par la subvention de la National Geographic Society WW-136R-17. LL et RV ont été partiellement financés par CONICET.

Informations sur l'auteur

Affiliations

École de géographie, Université de Leeds, Leeds, LS2 9JT, Royaume-Uni
RJW Brienen, L. Caldwell et E. Gloor
Ministère des Forêts, de la Faune et des Parcs, Direction de la recherche forestière, 2700 rue Einstein, Québec, QC, G1P 3W8, Canada
L. Duchesne
Département de biologie environnementale et forestière, SUNY-ESF, Syracuse, New York, NY, 13210, États-Unis
S. Voelker
Laboratoire des Sciences du Climat et de l'Environnement, IPSL, CNRS / CEA / UVSQ, 91191, Gif sur Yvette, France
J. Barichivich
Instituto de Geografía, Pontificia Universidad Católica de Valparaíso, Valparaíso, Chili
J. Barichivich
Département de l'agriculture et des sciences forestières (DAFNE), Université de Tuscia, 01100, Viterbe, Via SC de Lellis, Italie
M. Baliva, A. Di Filippo et G. Piovesan
Université de São Paulo, Institut des biosciences, Département de botanique, Rua do Matão, 277, São Paulo, SP, 05508-090, Brésil
G. Ceccantini et GM Locosselli
Natural Resources Institute Finland, Ounasjoentie 6, 96200, Rovaniemi, Finlande
S. Helama
Instituto Argentino de Nivología, Glaciología y Ciencias Ambientales (IANIGLA), CONICET-Mendoza, CC 330, (5500), Mendoza, Argentine
L. Lopez et R. Villalba
Instituto Nacional de Pesquisas Da Amazônia (INPA), Coordenação de Dinâmica Ambiental (CODAM), Av. André Araújo 2936, 69067-375, Manaus, Brésil
J. Schöngart

Contributions

RJWB, EG et LC ont conçu cette étude, RJWB et EG ont rédigé l'article, RJWB, LC et EG ont effectué des contrôles, des analyses et des simulations de données, JB et SV ont contribué aux téléchargements et contrôles de données ITRDB, LD, SV, MB, GC, AD , SH, GL, LL, GP, JS, RV ont contribué aux données, et tous les auteurs ont commenté l'article.

Les Enjeux qui m'intéressent (tous les articles)

Rechercher dans ce blog